迪杰斯特拉算法 Dijkstra

2022-05-16 约 2432 字预计阅读 5 分钟

戴克斯特拉算法（英语：Dijkstra’s algorithm），又译迪杰斯特拉算法，亦可不音译而称为Dijkstra算法，是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年发现的算法，并于3年后在期刊上发表。戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。

该算法存在很多变体：戴克斯特拉的原始版本仅适用于找到两个顶点之间的最短路径，后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径，产生一个最短路径树。

/images/algorithm/dijkstra/Dijkstra_Animation.gif — 迪杰斯特拉算法

起点以左下角的红点，目标是右上角的绿点，中间灰色的倒L型为障碍物。蓝色空圈表示"暂定"，用以搜索下一步；已经填充颜色的表示探访过，图中颜色以红到绿，越绿表示离起点越远。所有节点都被均匀的探索。

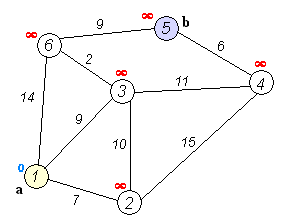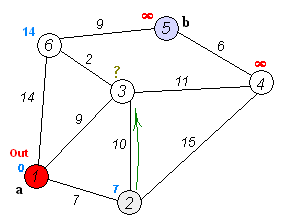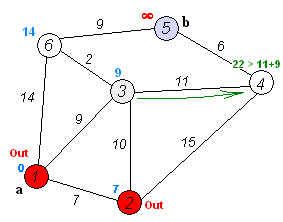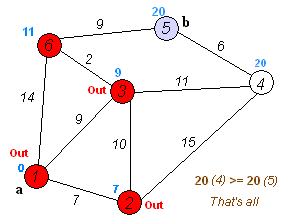
加权有向图，没有负权重边。

Dijkstra算法只能求取边的权重为非负的图的最短路径，而Bellman-Ford算法可以求取边的权重为负的图的最短路径（但Bellman-Ford算法在图中存在负环的情况下，最短路径是不存在的（负无穷））。

最短路径算法的思路可以由BFS算法进行扩展，之前我们学习过二叉树的层序遍历和网格型BFS的方法，BFS其实就是while循环里面套for循环。其中while循环控制一层一层往下走，for循环控制遍历每一层的节点。BFS算法处理的是无权图的搜索问题，所谓无权图，可以认为每条边的权重是1，从start起点到任意一个节点之间的路径权重就是它们之间“边”的条数。但是到了加权图这里，情况就变了，可能从start到end只需要走一步，但是这1步权重特别大，最短的路径其实要走很多步。

算法框架

朴素 Dijkstra（邻接矩阵）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


public class Graph {

  int[] dijkstra(int[][] graph, int start) {
    // 起始先将所有的点标记为「未更新」和「距离为正无穷」
        int n = graph.length;
       // dist[x] = y 代表从「源点/起点」到 x 的最短距离为 y
        int[] dist = new int[n];
        Arrays.fill(dist, INF);
        dist[start] = 0;
            // 记录哪些点已经被更新过
        boolean[] used = new boolean[n];
        for (int i = 0; i < n; i++) {
            int x = -1;
            for (int y = 0; y < n; ++y) {
              // 未被访问，且离起点最小的节点序号
                if (!used[y] && (x == -1 || dist[y] < dist[x])) {
                    x = y;
                }
            }
            used[x] = true;
            for (int y = 0; y < n; ++y) {
                dist[y] = Math.min(dist[y], dist[x] + g[x][y]);
            }
        }
      return dist;
  }

  public void init(){
    // 初始化邻接矩阵
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                w[i][j] = w[j][i] = i == j ? 0 : INF;
            }
        }
  }
}

以下是堆优化的 Dijkstra 算法。

1

int[] dijkstra(int[][] graph, int start)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


// 以 (点编号, 到起点的距离) 进行存储，优先弹出「最短距离」较小的点
public class State {
    // 节点 id
    public int id;
    // 当前节点距离起点的距离
    public int distFromStart;
    public State(int id, int distFromStart) {
        this.id = id;
        this.distFromStart = distFromStart;
    }
    public int getId() {
      return id;
    }
    public int getDistFromStart() {
      return distFromStart;
    }
}

邻接矩阵表示

这里用邻接矩阵，即二维数组 graph[][]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47


private int[] dijkstra(int[][] graph, int start) {
    // 记录最短路径的权重，可以理解为 DP table
    // ret[i] 的值就是节点 start 到节点 i 的最短路径权重
    int[] ret = new int[graph.length];

    Arrays.fill(ret, Integer.MAX_VALUE);

    ret[start] = 0;
    // 优先级队列 distFromStart 较小的排在前面
    PriorityQueue<State> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o.distFromStart));
    // 从起点开始进行  BFS
    queue.offer(new State(start, 0));
    while (!queue.isEmpty()) {
      State curNode = queue.poll();
      int curNodeId = curNode.getId();
      int curNodeDistFromStart = curNode.getDistFromStart();
      // 将curNode 的领接节点装入队列
      for (int nextNodeId : getNextNodes(graph, curNodeId)) {
        // 看看 从 curNode 达到 nextNode 的距离是否会更短
        int nextNodeDistFromStart = curNodeDistFromStart + graph[curNodeId][nextNodeId];
        if (nextNodeDistFromStart < ret[nextNodeId]) {
          // 将节点以及距离放入队列
          queue.offer(new State(nextNodeId, nextNodeDistFromStart));
          // 更新  dp table
          ret[nextNodeId] = nextNodeDistFromStart;
        }
      }
    }

    return ret;
  }

  /**
   * 邻接节点
   *
   * @param id 当前节点 Id
   * @return 返回当前节点的邻接节点
   */
  private List<Integer> getNextNodes(int[][] graph, int id) {
    List<Integer> list = new ArrayList<>();
    for (int i = 0; i < graph.length; i++) {
      if (graph[id][i] != -1) {
        list.add(i);
      }
    }
    return list;
  }

领接表表示

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56


private int[] dijkstra(List<Integer>[] graph, int start) {
    // 记录最短路径的权重，可以理解为 DP table
    // distTo[i] 的值就是节点 start 到节点 i 的最短路径权重
    // 节点数量
    int n = graph.length;
    // 记录每个点到 start 的最短距离
    int[] distTo = new int[n];
    // 初始化为最大值
    Arrays.fill(distTo, Integer.MAX_VALUE);
    // start to start = 0
    distTo[start] = 0;
    // 优先级队列 distFromStart 较小的排在前面
    PriorityQueue<State> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o.distFromStart));
    // 从起点开始进行  BFS
    queue.offer(new State(start, 0));
    while (!queue.isEmpty()) {
      State curNode = queue.poll();
      int curNodeId = curNode.getId();
      int curNodeDistFromStart = curNode.getDistFromStart();

      // 将curNode 的领接节点装入队列
      for (int nextNodeId : getNextNodes(graph, curNodeId)) {
        // 看看 从 curNode 达到 nextNode 的距离是否会更短
        int nextNodeDistFromStart = curNodeDistFromStart + weight(graph, curNodeId, nextNodeId);
        if (nextNodeDistFromStart < distTo[nextNodeId]) {
          // 将节点以及距离放入队列
          queue.offer(new State(nextNodeId, nextNodeDistFromStart));
          // 更新  dp table
          distTo[nextNodeId] = nextNodeDistFromStart;
        }
      }
    }

    return distTo;
  }

  /**
   * 权重函数
   *
   * @param from from 顶点
   * @param to to 顶点
   * @return 返回 from -> to 权重
   */
  private int weight(List<Integer>[] graph, int from, int to) {
    return graph[from].get(to);
  }

  /**
   * 邻接节点
   *
   * @param id 当前节点 Id
   * @return 返回当前节点的邻接节点
   */
  private List<Integer> getNextNodes(List<Integer>[] graph, int id) {
    return graph[id];
  }

Dijkstra算法本质上是一种贪心算法

朴素实现
优先队列(堆)优化

算法题

网络延迟时间

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2;
        int[][] g = new int[n][n];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(g[i], INF);
        }
        for (int[] t : times) {
            int x = t[0] - 1, y = t[1] - 1;
            g[x][y] = t[2];
        }

        int[] dist = new int[n];
        Arrays.fill(dist, INF);
        dist[k - 1] = 0;
        boolean[] used = new boolean[n];
        for (int i = 0; i < n; ++i) {
            int x = -1;
            for (int y = 0; y < n; ++y) {
                if (!used[y] && (x == -1 || dist[y] < dist[x])) {
                    x = y;
                }
            }
            used[x] = true;
            for (int y = 0; y < n; ++y) {
                dist[y] = Math.min(dist[y], dist[x] + g[x][y]);
            }
        }

        int ans = Arrays.stream(dist).max().getAsInt();
        return ans == INF ? -1 : ans;
    }
}

使用一个小根堆来寻找「未确定节点」中与起点距离最近的点。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2;
        List<int[]>[] g = new List[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new ArrayList<int[]>();
        }
        for (int[] t : times) {
            int x = t[0] - 1, y = t[1] - 1;
            g[x].add(new int[]{y, t[2]});
        }

        int[] dist = new int[n];
        Arrays.fill(dist, INF);
        dist[k - 1] = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> a[0] != b[0] ? a[0] - b[0] : a[1] - b[1]);
        pq.offer(new int[]{0, k - 1});
        while (!pq.isEmpty()) {
            int[] p = pq.poll();
            int time = p[0], x = p[1];
            if (dist[x] < time) {
                continue;
            }
            for (int[] e : g[x]) {
                int y = e[0], d = dist[x] + e[1];
                if (d < dist[y]) {
                    dist[y] = d;
                    pq.offer(new int[]{d, y});
                }
            }
        }

        int ans = Arrays.stream(dist).max().getAsInt();
        return ans == INF ? -1 : ans;
    }
}

复杂度分析

枚举写法的复杂度如下：

时间复杂度：$O(n^2+m)$，其中 m 是数组 times 的长度。
空间复杂度：$O(n^2)$。邻接矩阵需占用 $O(n^2)$ 的空间。

堆的写法复杂度如下：

时间复杂度：$O(mlogm)$，其中 m 是数组 times 的长度。
空间复杂度：$O(n+m)$。

值得注意的是，由于本题边数远大于点数，是一张稠密图，因此在运行时间上，枚举写法要略快于堆的写法。

https://zh.wikipedia.org/zh-cn/戴克斯特拉算法

目录