Kruskal 克鲁斯克尔算法

Kruskal 算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪心算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

步骤

1. 新建图 $G$，$G$ 中拥有原图中相同的节点，但没有边
2. 将原图中所有的边按权值从小到大排序
3. 从权值最小的边开始，如果这条边连接的两个节点于图 $G$ 中不在同一个连通分量中，则添加这条边到图 $G$ 中
4. 重复3，直至图 $G$ 中所有的节点都在同一个连通分量中

证明

• 这样的步骤保证了选取的每条边都是桥，因此图 $G$ 构成一个树。

• 为什么这一定是最小生成树呢？关键还是步骤3中对边的选取。算法中总共选取了 n-1 条边，每条边在选取的当时，都是连接两个不同的连通分量的权值最小的边

• 要证明这条边一定属于最小生成树，可以用反证法：如果这条边不在最小生成树中，它连接的两个连通分量最终还是要连起来的，通过其他的连法，那么另一种连法与这条边一定构成了环，而环中一定有一条权值大于这条边的边，用这条边将其替换掉，图仍旧保持连通，但总权值减小了。也就是说，如果不选取这条边，最后构成的生成树的总权值一定不会是最小的。

• 类别 最小生成树

• 数据结构 并查集

• 平均时间复杂度为 $O(|E|log|V|)$

• 空间复杂度 $\Omega (|E|+|V|)$

伪代码

1
2
3
4
5
6
7
8
9

KRUSKAL-FUNCTION(G, w)
  F := 空集合
  for each 图 G 中的顶点 v
    do 将 v 加入森林 F
  所有的边(u, v) ∈ E依权重 w 递增排序
  for each 边(u, v) ∈ E
    do if u 和 v 不在同一棵子树
      then F := F ∪ {(u, v)}
        将 u 和 v 所在的子树合并

概念

首先弄清楚最小生成树概念之前，请先弄清楚 「生成子图」「树」「生成树」概念

• 生成子图：一个图的生成子图指顶点集相同，边集可不同的子图
• 树：不含圈的连通图称为树
• 生成树：若图 $G$ 的生成子图 $T$ 是树，则称 $T$ 为 $G$ 的生成树
• 最小生成子树：在连通赋权图 $G$ 中，边权之和最小的生成树称为 $G$ 的最小生成树

可利用图的连通性来解决最小生成树的问题，很容易想到可以运用「并查集」算法来辅助生成最小生成树

问题一：如何判断一个图是否为原图的生成子图

利用并查集的连通分支的数量来判断

设顶点集的数量为 n，并查集中的节点数同为 n，一一对应

若最终并查集的连通分支数量为 1，则表明所有节点都在同一连通分支中，即子图为生成子图；反之则在多个分支中

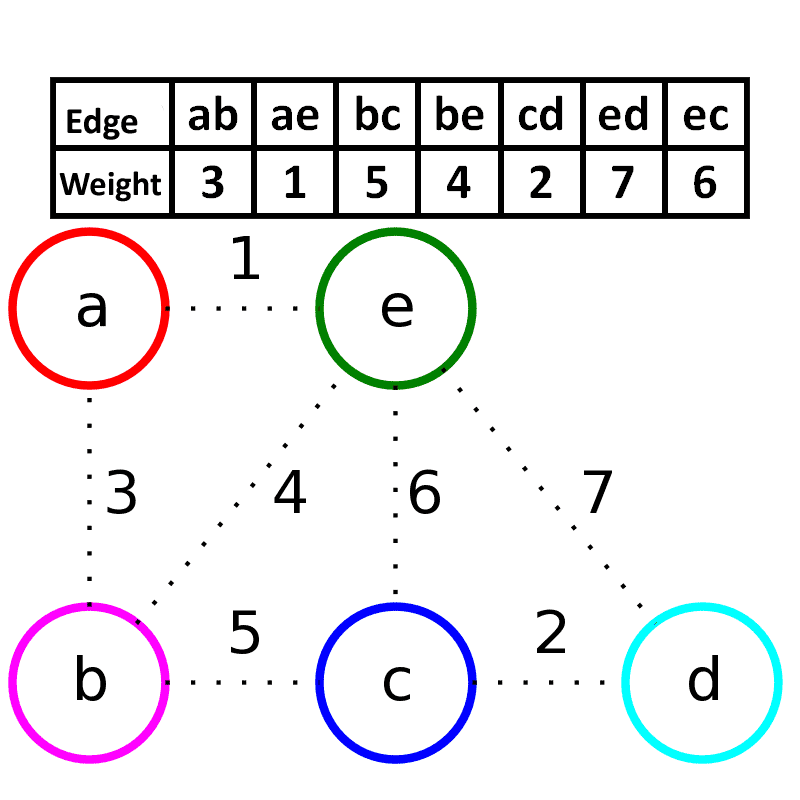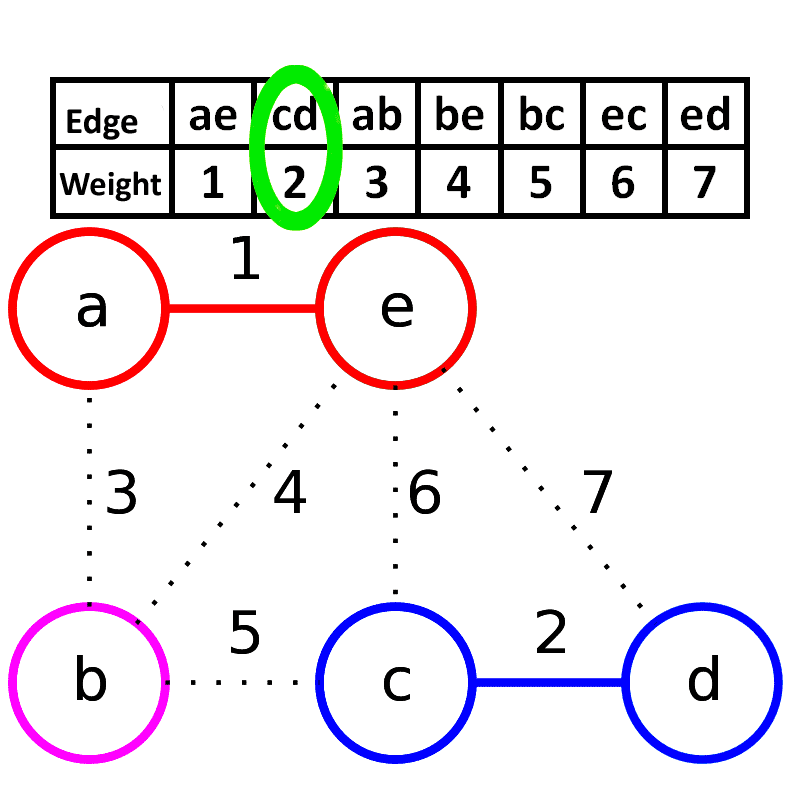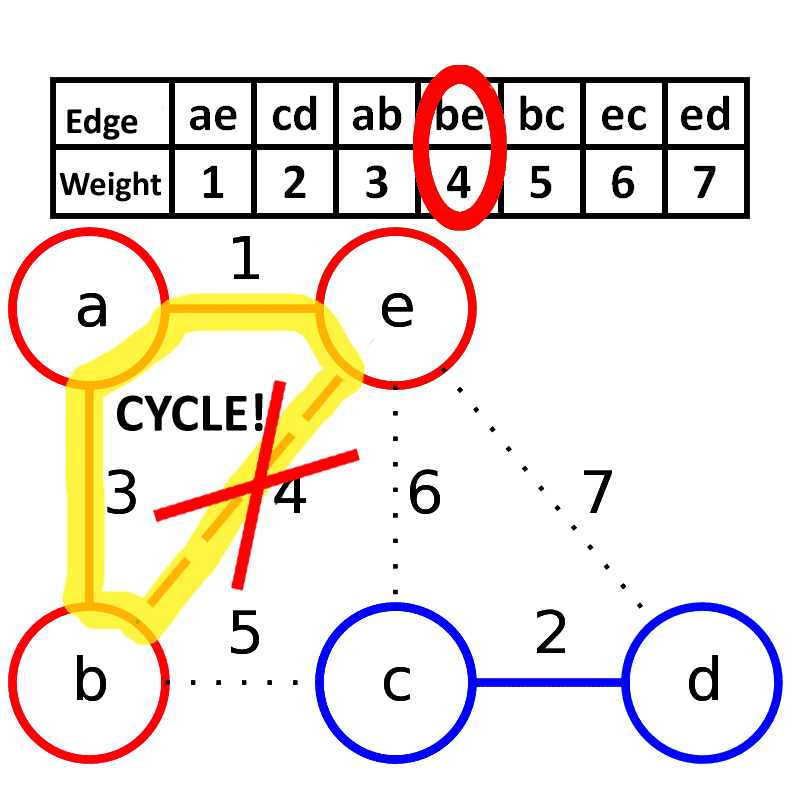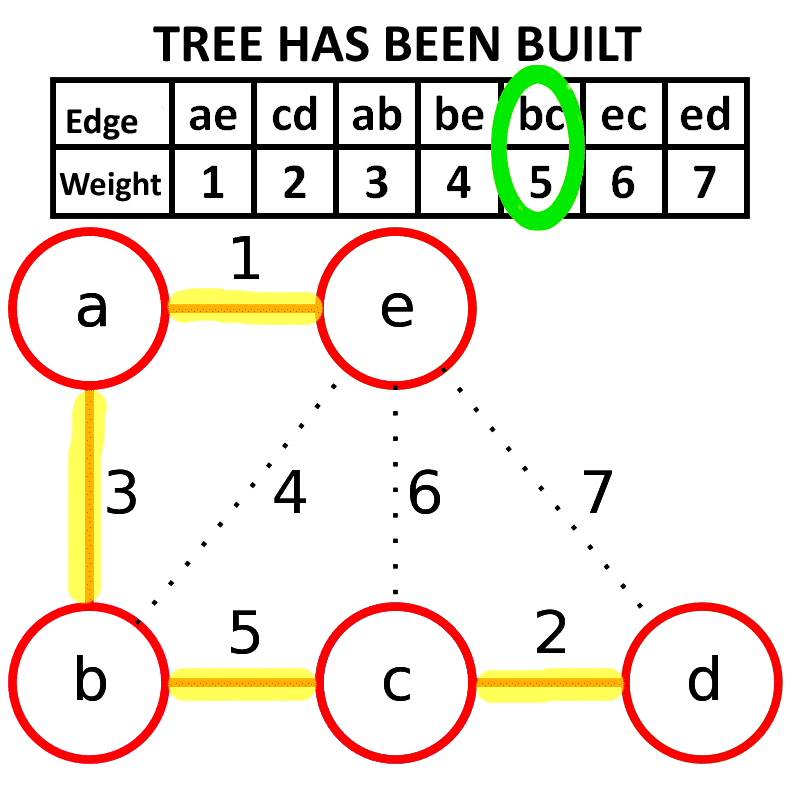
总结就是，对于添加的这条边，如果该边的两个节点本来就在同一连通分量里，那么添加这条边会产生环；反之，如果该边的两个节点不在同一连通分量里，则添加这条边不会产生环

问题二：如何判断生成子图是一棵树

利用并查集的连通性来判断

显而易见，如果在一个连通分支中，新增一条边，则会出现环/圈

故每次进行 union(u,v) 操作时前进行判断，如果 connected(u,v)==true，则跳过。这样就可以保证生成子图是一棵树

问题三：如何获得最小生成树

对边进行非递减排序，从权值小的开始得到生成子树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

int minimumCost(int n, int[][] edges) {
    // 编号为 0...n
    UF uf = new UF(n + 1);
    // 对所有边按照权重从小到大排序
    Arrays.sort(edges, (a, b) -> (a[2] - b[2]));
    // 记录最小生成树的权重之和
    int mst = 0;
    for (int[] edge : edges) {
        int u = edge[0];
        int v = edge[1];
        int weight = edge[2];
        // 若这条边会产生环，则不能加入 mst
        if (uf.connected(u, v)) {
            continue;
        }
        // 若这条边不会产生环，则属于最小生成树
        mst += weight;
        uf.union(u, v);
    }
    // 保证所有节点都被连通
    // uf.count() == 1 说明所有节点被连通
    return uf.count() == 1 ? mst : -1;
}

class UF {
    // 见 并查集的实现
}