并查集

2022-05-15 约 2293 字预计阅读 5 分钟

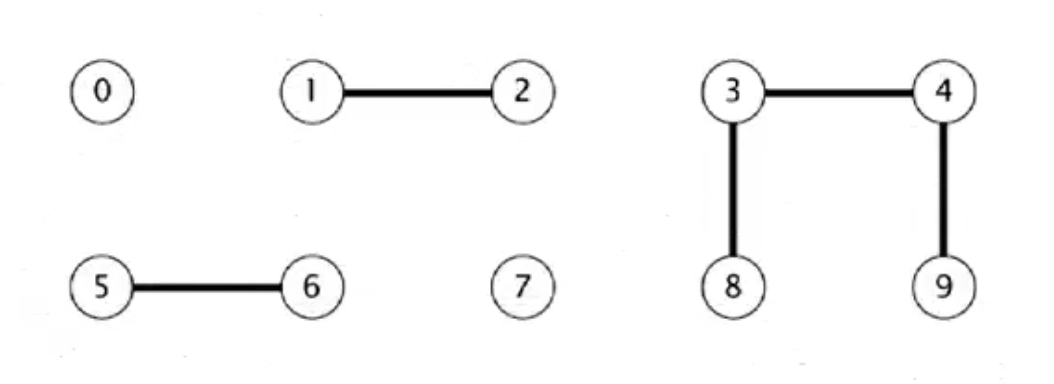
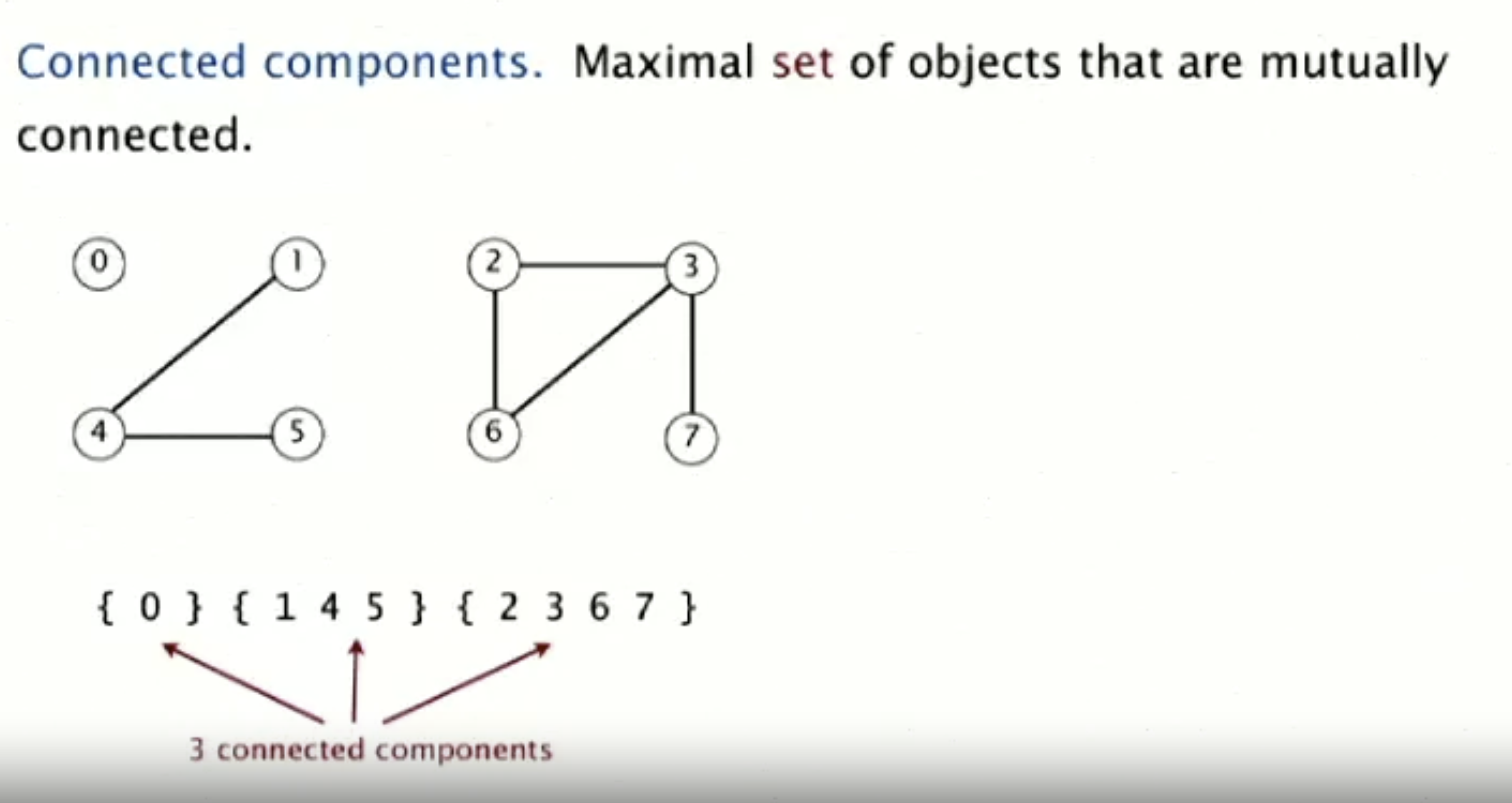
在计算机科学中，并查集（英文：Disjoint-set data structure，直译为不交集数据结构）是一种数据结构，用于处理一些不交集（Disjoint sets，一系列没有重复元素的集合）的合并及查询问题。

并查集支持如下操作：

查询：查询某个元素属于哪个集合，通常是返回集合内的一个“代表元素”。这个操作是为了判断两个元素是否在同一个集合之中。
合并：将两个集合合并为一个。
添加：添加一个新集合，其中有一个新元素。添加操作不如查询和合并操作重要，常常被忽略。

由于支持查询和合并这两种操作，并查集在英文中也被称为联合-查找数据结构（Union-find data structure）或者合并-查找集合（Merge-find set）。

“并查集” 可以用来指代任何支持上述操作的数据结构，但是一般来说，“并查集”特指其中最常见的一种实现：不交集森林（Disjoint-set forest）。经过优化的不交集森林有线性的空间复杂度（$O(n)$，n为元素数目，下同），以及接近常数的单次操作平均时间复杂度（$O(\alpha)$}，$\alpha$ 为反阿克曼函数），是效率最高的常见数据结构之一。

并查集是用于计算最小生成树的克鲁斯克尔(Kruskal)算法中的关键。由于最小生成树在网络路由等场景下十分重要，并查集也得到了广泛的引用。此外，并查集在符号计算，寄存器分配等方面也有应用。

不交集森林

不交集森林把每一个集合以一棵树表示，每一个节点即是一个元素。节点保存着到它的父节点的引用，树的根节点则保存一个空引用或者到自身的引用或者其他无效值，以表示自身为根节点。

并查集是来解决图的连通性问题

Union – 连接两个节点
Find – 查找所属的连通分量

所以，并查集主要就是实现以下接口：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class UF {
    /* 将 p 和 q 连接 */
    public void union(int p, int q);
    /* 判断 p 和 q 是否连通 */
    public boolean connected(int p, int q);
    /* 返回图中有多少个连通分量 每次建立连接减一 */
    public int count();
    
    /* 返回当前节点的根节点 */
    private int find(int x);
}

给定N个对象

Union 连接2个对象
Find/connected 判断2个对象是否有连接路径

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


union(4, 3);
union(3, 8);
union(6, 5);
union(9, 4);
union(2, 1);

connected(0, 7);  // false
connected(8, 9);  // true

union(5, 0);
union(7, 2);
union(6, 1);
union(1, 0);
connected(0, 7);  // true

数字图片的像素
网络中的计算机
社交网络中的好友
电脑芯片中的晶体管

编程时，命名对象为 0 ~ N-1

对象用 int 就像数组的 index
禁止与并查集无关的信息

建模连接

p 连接 q

对称性如果p 连接 q，那么 q 连接 p
传递性如果 p 连接 q 以及 q 连接 r，那么 p 连接 r

解法: 数组下标分组

数据结构

大小为 N 的 Integer 数组 id[]
说明：p 与 q 连接那么他们有相同的 id

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


public class QuickFindUF {

  private int[] id;

  public QuickFindUF(int N) {
    id = new int[N];
    for (int i = 0; i < N; i++) {
      id[i] = i;
    }
  }

  public boolean connected(int p, int q) {
    return id[p] == id[q];
  }

  public void union(int p, int q) {
    int pid = id[p];
    int qid = id[q];
    for (int i = 0; i < id.length; i++) {
      if (id[i] == pid) {
        id[i] = qid;
      }
    }
  }
}

解法: 数组存父节点构成森林，两个对象的 root 相同则连通

数据结构

大小为 N 的 Integer 数组 id[]
说明： id[i] 是 i 的父节点
Root(根节点) i = id[id[…id[i]…]]

数据结构数组，节点关系可以看成森林。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


public class QuickFindUF1 {

  private int[] id;

  public QuickFindUF1(int N) {
    id = new int[N];
    for (int i = 0; i < N; i++) {
      id[i] = i;
    }
  }

  private int root(int i) {
    while (i != id[i]) {
      i = id[i];
    }
    return i;
  }

  public boolean connected(int p, int q) {
    return root(p) == root(q);
  }

  public void union(int p, int q) {
    int i = root(p);
    int j = root(q);
    id[i] = j;
  }
}

给并查集加权重

避免树太高
记录每棵树的大小 (对象数)
连接比较小的数的 root 到大树的 root 来保持平衡

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


public class QuickFindUF2 {

  private int[] id;

  private int[] sz;

  public QuickFindUF2(int N) {
    id = new int[N];
    sz = new int[N];
    for (int i = 0; i < N; i++) {
      id[i] = i;
      sz[i] = 1;
    }
  }

  private int root(int i) {
    while (i != id[i]) {
      // 路径压缩
      id[i] = id[id[i]];
      i = id[i];
    }
    return i;
  }

  public boolean connected(int p, int q) {
    return root(p) == root(q);
  }

  public void union(int p, int q) {
    int i = root(p);
    int j = root(q);
    if (i == j) {
      return;
    }
    // 平衡性优化
    if (sz[i] < sz[j]) {
      id[i] = j;
      sz[j] += sz[i];
    } else {
      id[j] = i;
      sz[i] += sz[j];
    }
  }
}

被围绕的区域

并查集常用来解决连通性的问题，即将一个图中连通的部分划分出来。当我们判断图中两个点之间是否存在路径时，就可以根据判断他们是否在一个连通区域。

被围绕的区域

由于并查集我们一般用一维数组来记录，方便查找 parents，所以我们将二维坐标用函数转化为一维坐标。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


public void solve(char[][] board) {
    int m = board.length;
    int n = board[0].length;
    // 多一个节点用来存放 dummy
    UF uf = new UF(m * n + 1);
    int dummy = m * n;
    // 将 dummy 和四条边的所有 'O' 相连
    for (int i = 0; i < m; i++) {
        if (board[i][0] == 'O') uf.union(dummy, i * n);
        if (board[i][n - 1] == 'O') uf.union(dummy, i * n + n - 1);
    }
    for (int j = 0; j < n; j++) {
        if (board[0][j] == 'O') uf.union(dummy, j);
        if (board[m - 1][j] == 'O') uf.union(dummy, (m - 1) * n + j);
    }
    // 将内圈的所有相邻(上下左右)的 'O' 全部连起来 
    int[][] dirs = new int[][]{ {1, 0}, {0, 1}, {0, -1}, {-1, 0} };
    for (int i = 1; i < m - 1; i++) {
        for (int j = 1; j < n - 1; j++) {
            if (board[i][j] == 'O') {
                for (int[] d : dirs) {
                    int newI = i + d[0];
                    int newJ = j + d[1];
                    if (board[newI][newJ] == 'O') {
                        uf.union(i * n + j, newI * n + newJ);
                    }
                }
            }
        }
    }
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (board[i][j] == 'O' && !uf.connected(dummy, i * n + j)) board[i][j] = 'X';
        }
    }
}

最长连续序列

longest-consecutive-sequence

利用Map进行了一个「下标」和「值」的对应
利用Map进行重复元素的排除
利用Map可快速判断当前并查集中已有元素
将 num[i] 和 num[i] - 1 && num[i] + 1 相连

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59


class Solution {
    public int longestConsecutive(int[] nums) {

        Map<Integer, Integer> map = new HashMap<>();
        UF uf = new UF(nums.length);

        for (int i = 0; i < nums.length; i++) {
            // 存在重复元素，跳过
            if (map.containsKey(nums[i])) continue;

            if (map.containsKey(nums[i] - 1)) {
                uf.union(i, map.get(nums[i] - 1));
            }
            if (map.containsKey(nums[i] + 1)) {
                uf.union(i, map.get(nums[i] + 1));
            }
            map.put(nums[i], i);        
        }
        return uf.getMaxConnectSize();
    }
}
class UF {
    private int[] parent;
    private int[] size;

    public UF(int n) {
        parent = new int[n];
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) return;
        parent[rootP] = rootQ;
        // 注意 别写反了
        size[rootQ] += size[rootP];
    }
    // get root id
    private int find(int x) {
        while (x != parent[x]) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
    public int getMaxConnectSize() {
        int maxSize = 0;
        for (int i = 0; i < parent.length; i++) {
            if (i == parent[i]) {
                maxSize = Math.max(maxSize, size[i]);
            }
        }
        return maxSize;
    }
}

目录

并查集

不交集森林

建模连接

解法: 数组下标分组

解法: 数组存父节点构成森林，两个对象的 root 相同则连通

被围绕的区域

最长连续序列