skip list 跳跃列表
在计算机科学中,跳跃列表是一种数据结构。它使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是 $O(log n)$,优于数组的 $O(n)$ 复杂度。
快速的查询效果是通过维护一个多层次的链表实现的,且与前一层(下面一层)链表元素的数量相比,每一层链表中的元素的数量更少。一开始时,算法在最稀疏的层次进行搜索,直至需要查找的元素在该层两个相邻的元素中间。这时,算法将跳转到下一个层次,重复刚才的搜索,直到找到需要查找的元素为止。跳过的元素的方法可以是随机性选择或确定性选择,其中前者更为常见。
跳跃列表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃列表的算法有同平衡树一样的渐进的预期时间边界,并且更简单、更快速和使用更少的空间。
AVL树有着严格的O(logN)的查询效率,但是由于插入过程中可能需要多次旋转,导致插入效率较低,因而才有了在工程界更加实用的红黑树。
但是红黑树有一个问题就是在并发环境下使用不方便,比如需要更新数据时,Skip需要更新的部分比较少,锁的东西也更少,而红黑树有个平衡的过程,在这个过程中会涉及到较多的节点,需要锁住更多的节点,从而降低了并发性能。
它的最大优势是原理简单、容易实现、方便扩展、效率更高。
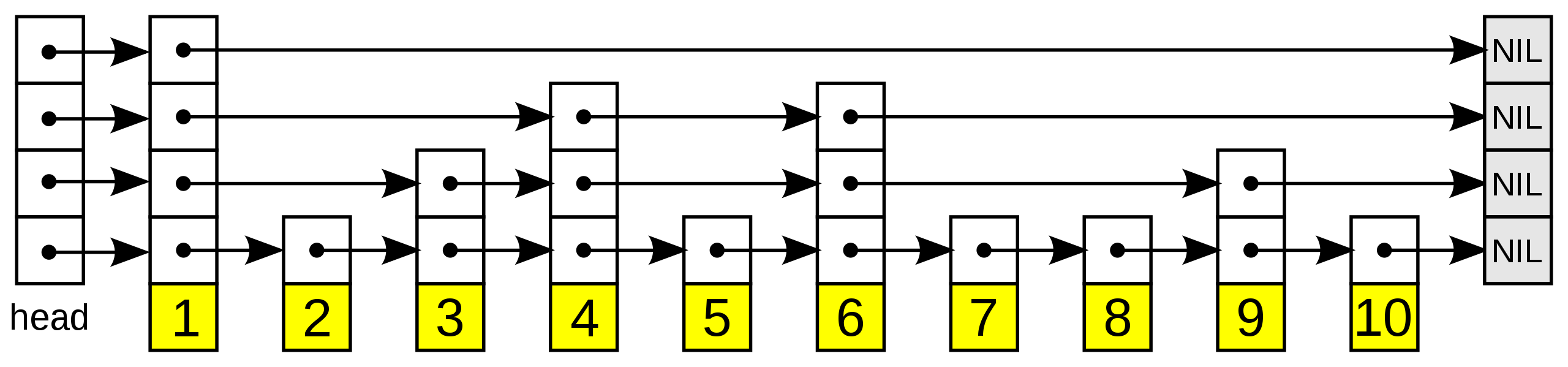
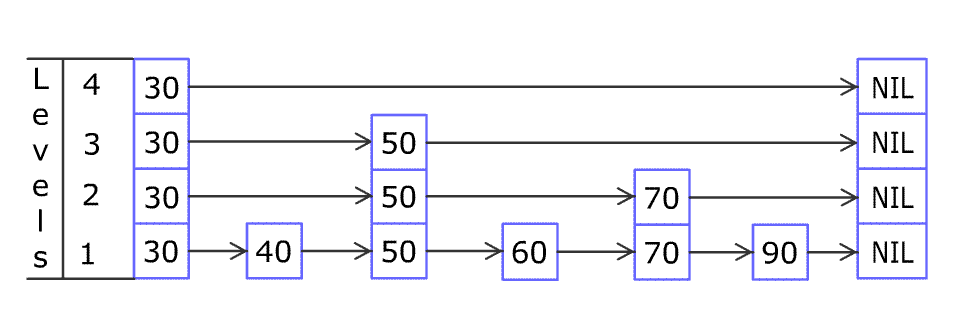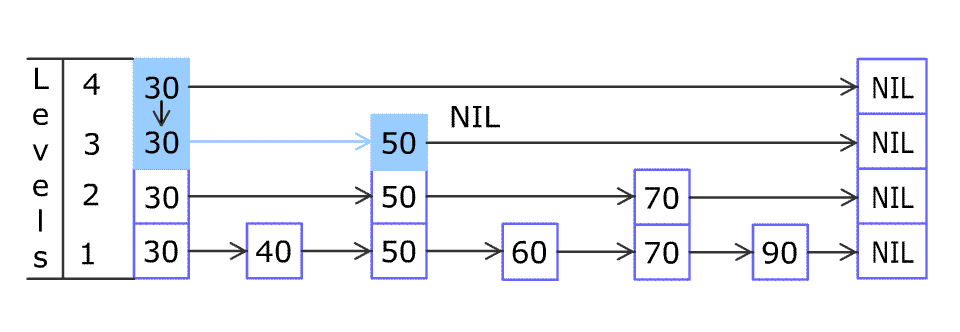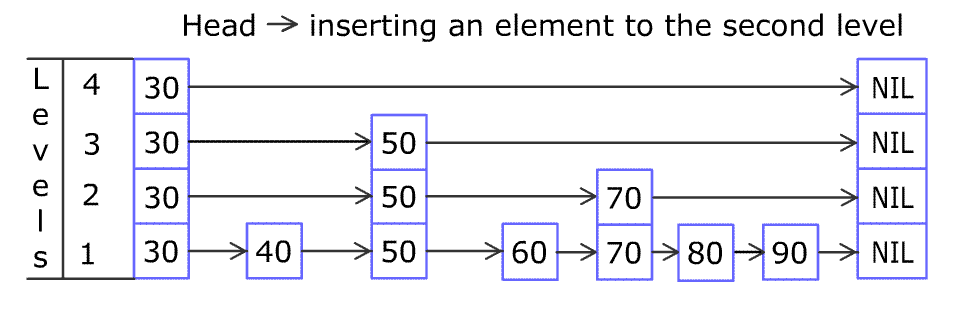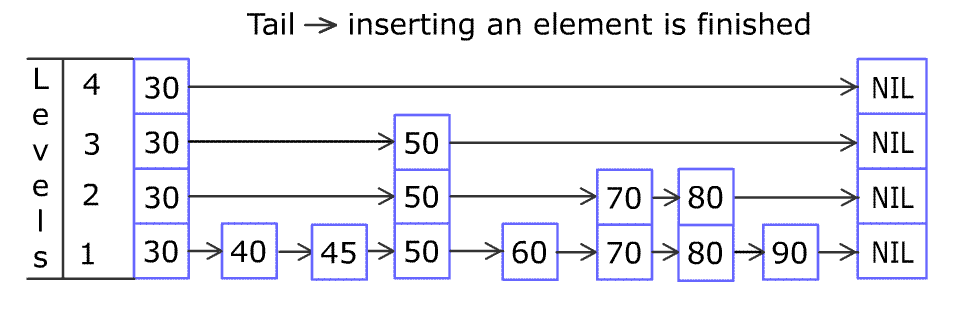
一张跳跃列表的示意图。每个带有箭头的框表示一个指针, 而每行是一个稀疏子序列的链表;底部的编号框(黄色)表示有序的数据序列。查找从顶部最稀疏的子序列向下进行, 直至需要查找的元素在该层两个相邻的元素中间。
| 算法 | 平均 | 最差 |
|---|---|---|
| 空间 | O(n) | O(n log n) |
| 搜索 | O(log n) | O(n) |
| 插入 | O(log n) | O(n) |
| 删除 | O(log n) | O(n) |
数据总数不一定是 $2^n$,插入删除也会破坏二分结构。 抛一枚硬币,花面朝上的可能性为 0.5,我们希望的严格二分,实质上就是任选跳跃表中的两层,上层的结点个数是下层结点个数的 1/2,也就是说下层的每个结点同时也是上层的结点的概率是 1/2,这不就和抛硬币花/字面朝上的概率是一致的嘛!
插入元素,先查找合适插入的位置,创建新的节点抛硬币决定是否在该插入位置往上建立新层。
应用
ConcurrentSkipListMap 和 ConcurrentSkipListSet 底层使用跳表数据结构来实现,跳表全称叫做跳跃表,它是一个随机化的数据结构,可以被看做二叉树的一个变种,通过使用“跳跃式”查找的方式使得插入、读取数据时复杂度变成了 $O(logn)$。
因此在一些热门的项目里用来替代平衡树,如 Redis、LevelDB等。
- Redis 中的 Sorted sets