在计算机科学中,trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
Trie这个术语来自于retrieval。根据词源学,trie的发明者Edward Fredkin把它读作/ˈtriː/ “tree”。但是,其他作者把它读作/ˈtraɪ/ “try”。
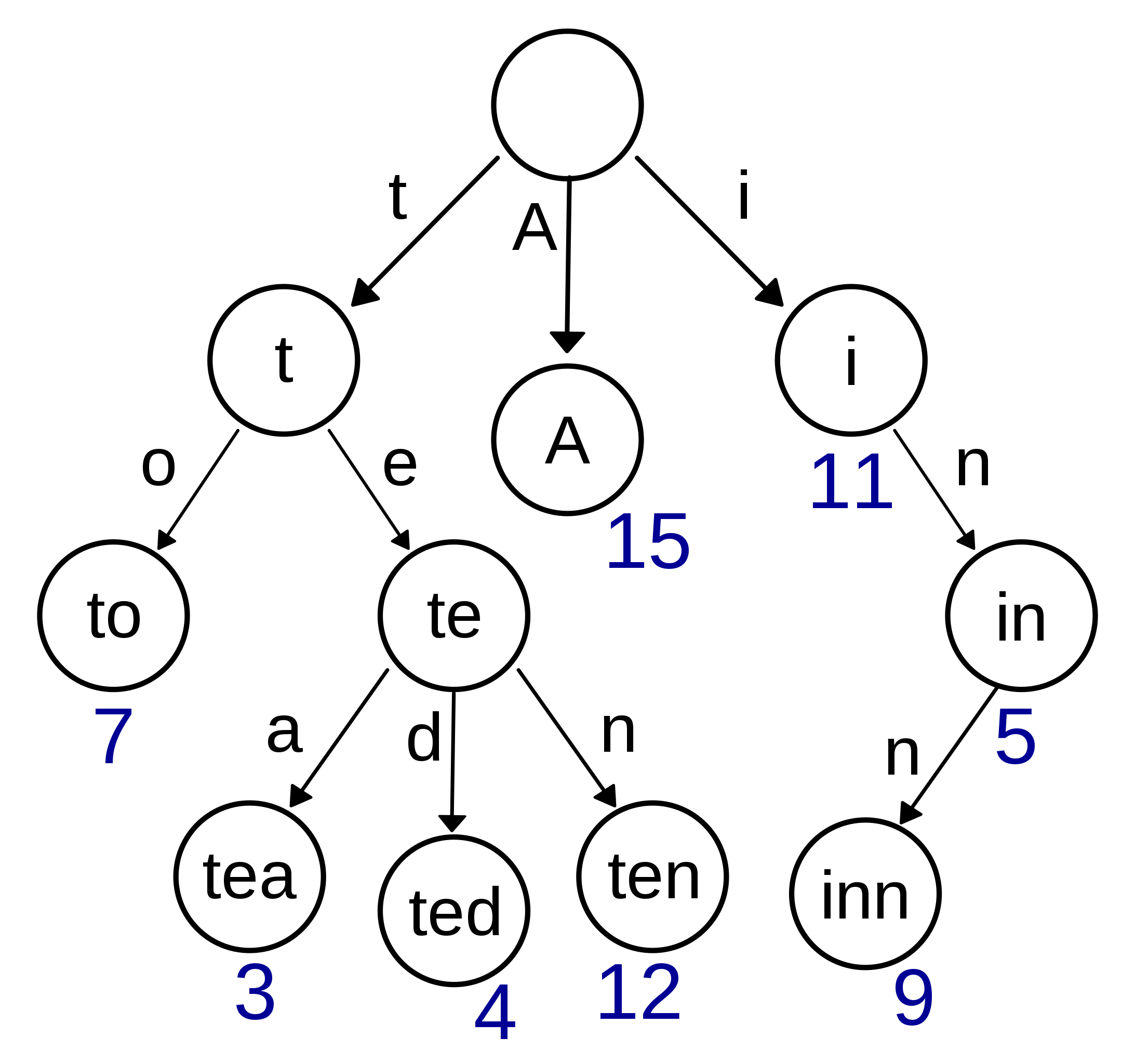
 8个键的 trie
8个键的 trie
一个保存了8个键的trie结构,“A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”.
在图示中,键标注在节点中,值标注在节点之下。每一个完整的英文单词对应一个特定的整数。Trie可以看作是一个确定有限状态自动机,尽管边上的符号一般是隐含在分支的顺序中的。
键不需要被显式地保存在节点中。图示中标注出完整的单词,只是为了演示trie的原理。
trie中的键通常是字符串,但也可以是其它的结构。trie的算法可以很容易地修改为处理其它结构的有序序列,比如一串数字或者形状的排列。比如,bitwise trie中的键是一串位元,可以用于表示整数或者内存地址。
应用
trie树常用于搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能。
实现方式
trie树实际上是一个确定有限状态自动机(DFA),通常用转移矩阵表示。行表示状态,列表示输入字符,(行,列)位置表示转移状态。这种方式的查询效率很高,但由于稀疏的现象严重,空间利用效率很低。也可以采用压缩的存储方式即链表来表示状态转移,但由于要线性查询,会造成效率低下。
于是人们提出了下面两种结构。
三数组Trie(Triple-Array Trie)结构包括三个数组:base,next和check.
二数组Trie(Double-Array Trie)包含base和check两个数组。base数组的每个元素表示一个Trie节点,即一个状态;check数组表示某个状态的前驱状态。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
class Trie {
// Alphabet size (# of symbols)
private static final int ALPHABET_SIZE = 26;
private Trie[] children;
private boolean isEnd;
public Trie() {
children = new Trie[ALPHABET_SIZE];
isEnd = false;
}
public void insert(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true;
}
public boolean search(String word) {
Trie node = searchPrefix(word);
return node != null && node.isEnd;
}
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;
}
private Trie searchPrefix(String prefix) {
Trie node = this;
for (int i = 0; i < prefix.length(); i++) {
char ch = prefix.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
return null;
}
node = node.children[index];
}
return node;
}
}
|